наверх | назад | вперед | содержание | предметный указатель функций
6 Предопределенные типы и классы
Haskell Prelude содержит предопределенные классы, типы и функции, которые неявно импортируются в каждую программу на Haskell. В этой главе мы опишем типы и классы, находящиеся в Prelude. Большинство функций не описаны здесь подробно, поскольку их назначение легко можно понять исходя из их определений, данных в главе 8. Другие предопределенные типы, такие как массивы, комплексные и рациональные числа, описаны в части II.6.1 Стандартные типы Haskell
Эти типы определены в Haskell Prelude. Числовые типы описаны в разделе 6.4. Там, где это возможно, дается определение типа на Haskell . Некоторые определения могут не быть полностью синтаксически правильными, но они верно передают смысл лежащего в основе типа.6.1.1 Булевский тип
data Bool = False | True deriving
(Read, Show, Eq, Ord, Enum, Bounded)
Булевский тип Bool является перечислением. Основные булевские функции --- это && (и), || (или) и not (не).
Имя otherwise (иначе) определено как True, чтобы сделать выражения, использующие стражи,
более удобочитаемыми.
6.1.2 Символы и строки
Символьный тип Char является перечислением, чьи значения представляют собой символы Unicode [11]. Лексический синтаксис для символов определен в разделе 2.6; символьные литералы --- это конструкторы без аргументов в типе данных Char. Тип Char является экземпляром классов Read, Show, Eq, Ord, Enum и Bounded. Функции toEnum и fromEnum, которые являются стандартными функциями из класса Enum, соответственно отображают символы в тип Int и обратно.
Обратите внимание, что каждый символ управления ASCII имеет несколько представлений в символьных литералах: в виде числовой эскейп-последовательности, в виде мнемонической эскейп-последовательности ASCII, и представление в виде \^X. Кроме того, равнозначны следующие литералы: \a и \BEL, \b и \BS, \f и \FF, \r и \CR, \t и \HT, \v и \VT и \n и \LF.
Строка --- это список символов:
type String = [Char]
Строки можно сократить, используя лексический синтаксис, описанный в
разделе 2.6. Например, "A string" является сокращением (аббревиатурой)
[ 'A',' ','s','t','r', 'i','n','g']
6.1.3 Списки
data [a] = [] | a : [a] deriving (Eq, Ord)
Списки --- это алгебраический тип данных для двух конструкторов, имеющих специальный синтаксис, описанных в разделе 3.7. Первый конструктор --- это пустой список, который обозначается `[]' ("nil"), второй --- это `:' ("cons"). Модуль PreludeList (см. раздел 8.1) определяет множество стандартных функций над списком. Арифметические последовательности и описание списка --- это два удобных синтаксиса, используемых для записи специальных видов списков, они описаны в разделах 3.10 и 3.11 соответственно. Списки являются экземпляром классов Read, Show, Eq, Ord, Monad, Functor и MonadPlus.
6.1.4 Кортежи
Кортежи --- это алгебраический тип данных со специальным синтаксисом, описанным в разделе 3.8. Тип каждого кортежа имеет один конструктор. Все кортежи являются экземплярами классов Eq, Ord, Bounded, Read, и Show (конечно, при условии, что все их составляющие типы являются экземплярами этих классов).
Нет никакой верхней границы размера кортежа, но некоторые реализации Haskell могут содержать ограничения на размер кортежей и на экземпляры, связанные с большими кортежами. Тем не менее, каждая реализация Haskell должна поддерживать кортежи вплоть до 15 размера, наряду с экземплярами классов Eq, Ord, Bounded, Read и Show. Prelude и библиотеки содержат определения функций над кортежами, таких как zip, для кортежей вплоть до 7 размера.
Конструктор для кортежа записывается посредством игнорирования выражений, соседствующих с запятыми; таким образом, (x,y) и (,) x y обозначают один и тот же кортеж. То же самое относится к конструкторам типов кортежей; таким образом, (Int,Bool,Int) и (,,) Int Bool Int обозначают один и тот же тип.
Следующие функции определены для пар (кортежей 2 размера): fst, snd, curry и uncurry. Для кортежей большего размера подобные функции не являются предопределенными.
6.1.5 Единичный тип данных
data () = () deriving (Eq, Ord, Bounded, Enum, Read, Show)
Единичный тип данных () имеет единственный, отличный от _|_, член --- конструктор без аргументов (). См. также раздел 3.9.
6.1.6 Типы функций
Функции --- это абстрактный тип: никакие конструкторы непосредственно не создают значения функций. В Prelude описаны следующие простые функции: id, const, (.), flip, ($) и until.6.1.7 Типы IO и IOError
Тип IO указывает на операции, которые взаимодействуют с внешним миром. Тип IO является абстрактным: никакие конструкторы не видны для пользователя. IO является экземпляром классов Monad и Functor. В главе 7 описываются операции ввода - вывода.Тип IOError является абстрактным типом, который представляет ошибки, вызванные операциями ввода - вывода. Он является экземпляром классов Show и Eq. Значения этого типа создаются различными функциями ввода - вывода. Более подробная информация о значениях в этом описании не представлена. Prelude содержит несколько функций ввода - вывода (определены в разделе 8.3). Гораздо больше функций ввода - вывода содержит часть II.
6.1.8 Другие типы
data Maybe a = Nothing | Just a deriving (Eq, Ord, Read, Show)
data Either a b = Left a | Right b deriving (Eq, Ord, Read, Show)
data Ordering = LT | EQ | GT deriving
(Eq, Ord, Bounded, Enum, Read, Show)
Тип Maybe является экземпляром классов Functor, Monad и MonadPlus. Тип Ordering используется функцией compare в классе Ord. Функции maybe и either описаны в Prelude.
6.2 Строгое вычисление
Применение функций в Haskell не является строгим, то есть аргумент функции вычисляется только тогда, когда требуется значение. Иногда желательно вызвать вычисление значения, используя функцию seq :seq :: a -> b -> b
Функция seq определена уравнениями:
| seq _|_b = _|_ |
| seq a b = b, if a /=_|_ |
Функция seq обычно вводится для того, чтобы улучшить производительность за счет избежания ненужной ленивости. Строгие типы данных (см. раздел 4.2.1) определены в терминах оператора $!. Тем не менее, наличие функции seq имеет важные семантические последствия, потому что эта функция доступна для каждого типа. Как следствие, _|_ --- это не то же самое, что \x -> _|_, так как можно использовать seq для того, чтобы отличить их друг от друга. По той же самой причине существование seq ослабляет параметрические свойства Haskell.
Оператор $! является строгим (вызываемым по значению)
применением, он определен
в терминах seq. Prelude также содержит определение оператора $ для выполнения нестрогих применений.
infixr 0 $, $!
($), ($!) :: (a -> b) -> a -> b
f $ x = f x
f $! x = x `seq` f x
Наличие оператора нестрогого применения $ может казаться избыточным, так как
обычное применение (f x) означает то же самое, что (f $ x).
Тем не менее, $ имеет низкий приоритет и правую ассоциативность,
поэтому иногда круглые скобки можно опустить, например:
f $ g $ h x = f (g (h x))
Это также полезно в ситуациях более высокого порядка, таких как map ($ 0) xs
или zipWith ($) fs xs.
6.3 Стандартные классы Haskell
На рис. 6.1 изображена иерархия классов Haskell , определенных в Prelude, и типы из Prelude, которые являются экземплярами этих классов.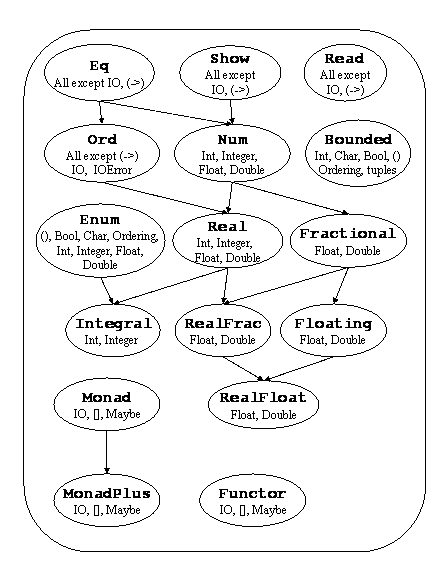
Рис. 5Стандартные классы Haskell |
Для многих методов в стандартных классах предусмотрены заданные по умолчанию объявления методов класса (раздел 4.3). Комментарий, данный для каждого объявления class в главе 8, определяет наименьшую совокупность определений методов, которые вместе с заданными по умолчанию объявлениями обеспечивают разумное определение для всех методов класса. Если такого комментария нет, то для того, чтобы полностью определить экземпляр, должны быть заданы все методы класса.
6.3.1 Класс Eq
class Eq a where
(==), (/=) :: a -> a -> Bool
x /= y = not (x == y)
x == y = not (x /= y)
Класс Eq предоставляет методы для сравнения на равенство (==) и неравенство (/=). Все основные типы данных, за исключением функций и IO, являются экземплярами этого класса. Экземпляры класса Eq можно использовать для выведения любого определяемого пользователем типа данных, чьи компоненты также являются экземплярами класса Eq.
Это объявление задает используемые по умолчанию объявления методов /= и ==, каждый из которых определен в терминах другого. Если объявление экземпляра класса Eq не содержит описания ни одного из перечисленных методов, тогда оба метода образуют петлю. Если определен один из методов, то другой, заданный по умолчанию метод, будет использовать тот, который определен. Если оба метода определены, заданные по умолчанию методы использоваться не будут.
6.3.2 Класс Ord
class (Eq a) => Ord a where
compare :: a -> a -> Ordering
(<), (<=), (>=), (>) :: a -> a -> Bool
max, min :: a -> a -> a
compare x y | x == y = EQ
| x <= y = LT
| otherwise = GT
x <= y = compare x y /= GT
x < y = compare x y == LT
x >= y = compare x y /= LT
x > y = compare x y == GT
-- Заметьте, что (min x y, max x y) = (x,y) или (y,x)
max x y | x <= y = y
| otherwise = x
min x y | x <= y = x
| otherwise = y
Класс Ord используется для полностью упорядоченных типов данных. Все основные типы данных, за исключением функций, IO и IOError, являются экземплярами этого класса. Экземпляры класса Ord можно использовать для выведения любого определяемого пользователем типа данных, чьи компоненты находятся в Ord. Объявленный порядок конструкторов в объявлении данных определяет порядок в производных экземплярах класса Ord. Тип данных Ordering позволяет использовать единообразное сравнение для определения точного порядка двух объектов.
Заданные по умолчанию объявления позволяют пользователю создавать экземпляры класса Ord посредством функции compare с определенным типом или функций == и <= с определенным типом.
6.3.3 Классы Read и Show
type ReadS a = String -> [(a,String)]
type ShowS = String -> String
class Read a where
readsPrec :: Int -> ReadS a
readList :: ReadS [a]
-- ... объявление readList по умолчанию дано в Prelude
class Show a where
showsPrec :: Int -> a -> ShowS
show :: a -> String
showList :: [a] -> ShowS
showsPrec _ x s = show x ++ s
show x = showsPrec 0 x ""
-- ... объявление для showList по умолчанию дано в Prelude
Классы Read и Show используются для преобразования значений к типу строка или преобразования строк к другим значениям. Аргумент типа Int в функциях showsPrec и readsPrec задает приоритет внешнего контекста (см. раздел 10.4).
showsPrec и showList возвращают функцию, действующую из String в String, которая обеспечивает постоянную конкатенацию их результатов посредством использования композиции функций. Также имеется специализированный вариант show, который использует нулевой приоритет контекста и возвращает обычный String. Метод showList предназначен для того, чтобы предоставить программисту возможность задать специализированный способ представления списков значений. Это особенно полезно для типа Char, где значения типа String должны быть представлены в двойных кавычках, а не в квадратных скобках.
Производные экземпляры классов Read и Show копируют стиль, в котором объявлен конструктор: для ввода и вывода используются инфиксные конструкторы и имена полей. Строки, порождаемые showsPrec, обычно могут быть прочитаны readsPrec.
Все типы Prelude, за исключением функциональных типов и типов IO, являются экземплярами классов Show и Read. (Если желательно, программист может легко сделать функции и типы IO (пустыми) экземплярами класса Show, обеспечив объявление экземпляра.)
Для удобства использования Prelude обеспечивает следующие вспомогательные
функции:
reads :: (Read a) => ReadS a
reads = readsPrec 0
shows :: (Show a) => a -> ShowS
shows = showsPrec 0
read :: (Read a) => String -> a
read s = case [x | (x,t) <- reads s, ("","") <- lex t] of
[x] -> x
[] -> error "PreludeText.read: нет разбора"
_ -> error "PreludeText.read: неоднозначный разбор"
shows и reads используют заданный по умолчанию нулевой приоритет. Функция read считывает ввод из строки, которая должна быть полностью потреблена процессом ввода.
Функция lex :: ReadS String, используемая функцией read, также является частью Prelude. Она считывает из ввода одну лексему, игнорируя пробельные символы перед лексемой, и возвращает символы, которые составляют лексему. Если входная строка содержит только пробельные символы, lex возвращает одну успешно считанную "лексему", состоящую из пустой строки. (Таким образом lex "" = [("","")].) Если в начале входной строки нет допустимой лексемы, lex завершается с ошибкой (т.е. возвращает []).
6.3.4 Класс Enum
class Enum a where
succ, pred :: a -> a
toEnum :: Int -> a
fromEnum :: a -> Int
enumFrom :: a -> [a] -- [n..]
enumFromThen :: a -> a -> [a] -- [n,n'..]
enumFromTo :: a -> a -> [a] -- [n..m]
enumFromThenTo :: a -> a -> a -> [a] -- [n,n'..m]
-- Заданные по умолчанию объявления даны в Prelude
Класс Enum определяет операции над последовательно упорядоченными типами. Функции succ и pred возвращают соответственно последующий и предшествующий элемент заданного значения. Функции fromEnum и toEnum преобразуют соответственно значения типа Enum к типу Int и значения типа Int к типу Enum. Методы, начинающиеся с enumFrom ..., используются при преобразовании арифметических последовательностей (раздел 3.10).
Экземпляры класса Enum можно использовать для выведения любого перечислимого типа (типы, чьи конструкторы не имеют полей), см. главу 10.
Для любого типа, который является экземпляром класса Bounded, а также экземпляром класса Enum, должны выполняться следующие условия:
- Вызовы succ maxBound и pred minBound должны завершаться
с ошибкой времени выполнения программы.
- fromEnum и toEnum должны завершаться с ошибкой
времени выполнения программы, если
значение результата не представимо в указанном типе результата. Например,
toEnum 7 :: Bool является ошибкой.
- enumFrom и enumFromThen должны быть определены с
неявным указанием границы, так:
enumFrom x = enumFromTo x maxBound
enumFromThen x y = enumFromThenTo x y bound
where
bound | fromEnum y >= fromEnum x = maxBound
| otherwise = minBound
Следующие типы Prelude являются экземплярами класса Enum:
- Перечислимые типы: (), Bool и Ordering.
Семантика этих экземпляров описана в главе 10.
Например, [LT..] --- список [LT,EQ,GT].
- Char: экземпляр описан в главе 8, базируется
на примитивных функциях, которые осуществляют преобразование между Char и Int.
Например, enumFromTo 'a' 'z' обозначает
список строчных букв в алфавитном порядке.
- Числовые типы: Int, Integer, Float, Double. Семантика этих экземпляров описана далее.
Для типов Int и Integer функции перечисления имеют следующий смысл:
- Последовательность enumFrom e1 --- это список [e1,e1+1,e1+2,...].
- Последовательность enumFromThen e1 e2 --- это список [e1,e1+i,e1+2i,...],
где приращение i равно e2-e1. Приращение может быть нулевое или отрицательное.
Если приращение равно нулю, все элементы списка совпадают.
- Последовательность enumFromTo e1 e3 --- это
список [e1,e1+1,e1+2,...e3].
Список пуст, если e1 > e3.
- Последовательность enumFromThenTo e1 e2 e3 --- это список [e1,e1+i,e1+2i,...e3], где приращение i равно e2-e1. Если приращение является положительным или нулевым, список заканчивается, когда следующий элемент будет больше чем e3; список пуст, если e1 > e3. Если приращение является отрицательным, список заканчивается, когда следующий элемент будет меньше чем e3; список пуст, если e1 < e3.
Для всех четырех числовых типов из Prelude все функции семейства enumFrom являются строгими по всем своим параметрам.
6.3.5 Класс Functor
class Functor f where
fmap :: (a -> b) -> f a -> f b
Класс Functor
используется для типов, для которых можно установить соответствие (задать отображение). Списки, IO и
Maybe входят в этот класс.
Экземпляры класса Functor должны удовлетворять следующим условиям:
| fmap id | = | id |
| fmap (f . g) | = | fmap f . fmap g |
Все экземпляры класса Functor, определенные в Prelude, удовлетворяют этим условиям.
6.3.6 Класс Monad
class Monad m where
(>>=) :: m a -> (a -> m b) -> m b
(>>) :: m a -> m b -> m b
return :: a -> m a
fail :: String -> m a
m >> k = m >>= \_ -> k
fail s = error s
Класс Monad определяет основные операции над монадами. Для получения дополнительной информации о монадах смотрите главу 7.
"do"-выражения предоставляют удобный синтаксис для записи монадических выражений (см. раздел 3.14). Метод fail вызывается при ошибке сопоставления с образцом в do-выражении.
В Prelude списки, Maybe и IO являются экземплярами класса Monad. Метод fail для списков возвращает пустой список [], для Maybe возвращает Nothing, а для IO вызывает заданное пользователем исключение в монаде IO (см. раздел 7.3).
Экземпляры класса Monad должны удовлетворять следующим условиям:
| return a >>= k | = | k a |
| m >>= return | = | m |
| m >>= (\x -> k x >>= h) | = | (m >>= k) >>= h |
Экземпляры классов Monad и Functor должны дополнительно удовлетворять условию:
| fmap f xs | = | xs >>= return . f |
Все экземпляры класса Monad, определенные в Prelude, удовлетворяют этим условиям.
Prelude обеспечивает следующие вспомогательные функции:
sequence :: Monad m => [m a] -> m [a]
sequence_ :: Monad m => [m a] -> m ()
mapM :: Monad m => (a -> m b) -> [a] -> m [b]
mapM_ :: Monad m => (a -> m b) -> [a] -> m ()
(=<<) :: Monad m => (a -> m b) -> m a -> m b
6.3.7 Класс Bounded
class Bounded a where
minBound, maxBound :: a
Класс Bounded используется для именования верхней и нижней границ типа. Класс Ord не является суперклассом класса Bounded, так как типы, которые не являются полностью упорядоченными, могут также иметь верхнюю и нижнюю границы. Типы Int, Char, Bool, (), Ordering и все кортежи являются экземплярами класса Bounded. Класс Bounded можно использовать для выведения любого перечислимого типа; minBound является первым в списке конструкторов объявления data, а maxBound --- последним. Класс Bounded можно также использовать для выведения типов данных, у которых один конструктор и типы компонентов находятся в Bounded.
6.4 Числа
Haskell предоставляет несколько видов чисел; на числовые типы и операции над ними сильно повлияли Common Lisp и Scheme. Имена числовых функций и операторы обычно перегружены посредством использования нескольких классов типов с отношением включения, которые изображены на рис. 6.1. Класс Num числовых типов является подклассом класса Eq, так как все числа можно сравнить на равенство; его подкласс Real также является подклассом класса Ord, так как остальные операции сравнения применимы ко всем числам, за исключением комплексных (определенных в библиотеке Complex). Класс Integral содержит целые числа ограниченного и неограниченного диапазона; класс Fractional содержит все нецелые типы; а класс Floating содержит все числа с плавающей точкой, действительные и комплексные.
В Prelude определены только наиболее основные числовые типы: целые числа фиксированной точности (Int), целые числа произвольной точности (Integer), числа с плавающей точкой одинарной точности (Float) и двойной точности (Double). Остальные числовые типы, такие как рациональные и комплексные числа, определены в библиотеках. В частности тип Rational --- это отношение двух значений типа Integer, он определен в библиотеке Ratio.
Заданные по умолчанию операции над числами с плавающей точкой, определенные в Haskell Prelude, не соответствуют текущим стандартам независимой от языка арифметики (LIA). Эти стандарты требуют значительно большей сложности в числовой структуре и потому были отнесены к библиотеке. Некоторые, но не все, аспекты стандарта IEEE чисел с плавающей точкой были учтены в классе RealFloat из Prelude.
Стандартные числовые типы перечислены в таблице 6.1. Тип Int целых чисел конечной точности охватывает по меньшей мере диапазон [ - 229, 229 - 1]. Поскольку Int является экземпляром класса Bounded, для определения точного диапазона, заданного реализацией, можно использовать maxBound и minBound. Float определяется реализацией; желательно, чтобы этот тип был по меньшей мере равен по диапазону и точности типу IEEE одинарной точности. Аналогично, тип Double должен охватывать диапазон чисел IEEE двойной точности. Результаты исключительных ситуаций (таких как выход за верхнюю или нижнюю границу) для чисел фиксированной точности не определены; в зависимости от реализации это может быть ошибка ( _|_), усеченное значение или специальное значение, такое как бесконечность, неопределенность и т.д.
| Тип | Класс | Описание |
| Integer | Integral | Целые числа произвольной точности |
| Int | Integral | Целые числа фиксированной точности |
| (Integral a) => Ratio a | RealFrac | Рациональные числа |
| Float | RealFloat | Действительные числа с плавающей точкой одинарной точности |
| Double | RealFloat | Действительные числа с плавающей точкой двойной точности |
| (RealFloat a) => Complex a | Floating | Комплексные числа с плавающей точкой |
Таблица 2
Стандартные числовые типы
Стандартные классы чисел и другие числовые функции, определенные в Prelude, изображены на рис. 6.2 - 6.3. На рис. 6.1 показаны зависимости между классами и встроенными типами, которые являются экземплярами числовых классов.
Рис. 7Стандартные классы чисел и связанные с ними операции, часть 2 |
6.4.1 Числовые литералы
Синтаксис числовых литералов описан в
разделе 2.5. Целые литералы представляет собой
применение
функции fromInteger к соответствующему
значению типа
Integer. Аналогично, литералы с плавающей точкой обозначают
применение
fromRational к значению типа Rational (то есть
Ratio Integer). С учетом заданных типов
fromInteger :: (Num a) => Integer -> a
fromRational :: (Fractional a) => Rational -> a
целые литералы и литералы с плавающей точкой имеют
соответственно тип (Num a) => a и (Fractional a) => a.
Числовые литералы определены косвенным образом для того, чтобы их можно было
рассматривать как значения любого подходящего числового типа.
В разделе 4.3.4 рассматривается неоднозначность перегрузки.
6.4.2 Арифметические и теоретико-числовые операции
Инфиксные методы класса (+), (*), (-) и унарная функция negate (которая также может быть записана как знак минус, стоящий перед аргументом, см. раздел 3.4) применимы ко всем числам. Методы класса quot, rem, div и mod применимы только к целым числам, тогда как метод класса (/) применим только к дробным. Методы класса quot, rem, div и mod удовлетворяют следующим условиям, если y отличен от нуля:
| (x `quot` y)*y + (x `rem` y) == x |
| (x `div` y)*y + (x `mod` y) == x |
`quot` --- это деление нацело с округлением в сторону нуля,
тогда как результат `div` округляется в сторону
отрицательной бесконечности.
Метод класса quotRem принимает в качестве аргументов делимое и делитель
и возвращает пару (частное, остаток); divMod определен
аналогично:
quotRem x y = (x `quot` y, x `rem` y)
divMod x y = (x `div` y, x `mod` y)
Также для целых чисел определены предикаты even (четный) и odd (нечетный):
even x = x `rem` 2 == 0
odd = not . even
Наконец, имеются функции, которые возвращают наибольший общий делитель и наименьшее общее кратное.
gcd x y вычисляет наибольшее
(положительное) целое число, которое является делителем и x, и y, например, gcd (-3) 6 = 3, gcd (-3) (-6) = 3,
gcd 0 4 = 4. gcd 0 0 вызывает ошибку времени выполнения программы.
lcm x y вычисляет наименьшее положительное целое число, для которого и x, и y являются делителями.
6.4.3 Возведение в степень и логарифмы
Показательная функция exp и логарифмическая функция log принимают в качестве аргумента число с плавающей точкой и используют при вычислении основание e. logBase a x возвращает логарифм x по основанию a. sqrt возвращает арифметическое значение квадратного корня числа с плавающей точкой. Имеются три операции возведения в степень, каждая из которых принимает по два аргумента: (^) возводит любое число в неотрицательную целую степень, (^^) возводит дробное число в любую целую степень и (**) принимает два аргумента с плавающей точкой. Значение x^0 или x^^0 равно 1 для любого x, включая ноль; значение 0**y не определено.
6.4.4 Абсолюная величина и знак
Число имеет абсолютную величину
и знак. Функции abs и
signum применимы к любому числу и удовлетворяют условию:
abs x * signum x == x
Для действительных чисел эти функции определены следующим образом:
abs x | x >= 0 = x
| x < 0 = -x
signum x | x > 0 = 1
| x == 0 = 0
| x < 0 = -1
6.4.5 Тригонометрические функции
Класс Floating предоставляет функции для вычисления кругового и гиперболического синуса, косинуса, тангенса и обратных функций. Имеются реализации tan, tanh, logBase, ** и sqrt, заданные по умолчанию, но разработчики могут реализовать свои, более точные функции.
Класс RealFloat предоставляет версию функции для вычисления арктангенса, которая принимает два действительных аргумента с плавающей точкой. Для действительных чисел с плавающей точкой x и y atan2 y x вычисляет угол (от положительной оси X) вектора, проведенного из начала координат в точку (x,y). atan2 y x возвращает значение в диапазоне [-pi, pi]. При этом, в соответствии с семантикой Common Lisp для начала координат, поддерживются нули со знаком. atan2 y 1, где y находится в типе RealFloat, должен вернуть то же самое значение, что и atan y. Имеется заданное по умолчанию определение atan2, но разработчики могут реализовать свою, более точную функцию.
Точное определение вышеупомянутых функций такое же, как и в Common Lisp, которое, в свою очередь, соответствует предложению Пенфилда (Penfield) для APL [9]. Для подробного обсуждения ветвей, разрывностей и реализации смотрите эти ссылки.
6.4.6 Приведение и извлечение компонент
Каждая из функций ceiling, floor, truncate и round принимает в качестве аргумента действительное дробное число и возвращает целое число. ceiling x возвращает наименьшее целое число, которое не меньше чем x, floor x возвращает наибольшее целое число, которое не больше чем x. truncate x возвращает ближайшее к x целое число, которое находится между 0 и x включительно. round x возвращает ближайшее к x целое число, результат округляется в сторону четного числа, если x находится на одинаковом расстоянии от двух целых чисел.
Функция properFraction принимает в качестве аргумента действительное дробное число x и возвращает пару (n,f), такую, что x = n+f, где n --- целое число с тем же знаком, что и x, f --- дробное число с тем же типом и знаком, что и x, и с абсолютным значением меньше 1. Функции ceiling, floor, truncate и round можно определить в терминах properFraction.
Имеются две функции, которые осуществляют преобразование чисел к типу Rational: toRational возвращает рациональный эквивалент действительного аргумента с полной точностью; approxRational принимает два действительных дробных аргумента x и e и возвращает простейшее рациональное число, которое отличается от x не более чем на e, где рациональное число p/q , находящееся в приведенном виде, считается более простым, чем другое число p ' /q ' , если |p | <=|p ' | и q <=q ' . Каждый действительный интервал содержит единственное простейшее рациональное число, в частности, обратите внимание, что 0/1 является простейшим рациональным числом из всех.
Методы класса RealFloat предоставляют эффективный, машинонезависимый способ получить доступ к компонентам числа с плавающей точкой. Функции floatRadix, floatDigits и floatRange возвращают параметры типа с плавающей точкой: соответственно основание числового представления, количество цифр этого основания в мантиссе (значащей части числа) и наибольшее и наименьшее значения, которое может принимать экспонента. Функция decodeFloat, будучи примененной к действительному числу с плавающей точкой, возвращает мантиссу в виде числа типа Integer и соответствующую экспоненту (в виде числа типа Int). Если decodeFloat x возвращает (m,n), то x равно по значению mbn, где b --- основание с плавающей точкой, и, кроме того, либо m и n равны нулю, либо bd-1<=m<bd, где d --- значение floatDigits x. encodeFloat выполняет обратное преобразование. Функции significand и exponent вместе предоставляют ту же информацию, что и decodeFloat, но более точную, чем Integer, significand x возвращает значение того типа, что и x, но лежащее в пределах открытого интервала (-1,1). exponent 0 равно нулю. scaleFloat умножает число с плавающей точкой на основание, возведенное в целую степень.
Функции isNaN, isInfinite, isDenormalized, isNegativeZero и isIEEE поддерживают числа, представимые в соответствии со стандартом IEEE. Для чисел с плавающей точкой, не соответствующих стандарту IEEE, они могут вернуть ложное значение.
Также имеются следующие функции приведения:
fromIntegral :: (Integral a, Num b) => a -> b
realToFrac :: (Real a, Fractional b) => a -> b
Описание Haskell 98
наверх | назад | вперед | содержание | предметный указатель функций
Декабрь 2002